Last month, I published a post on the social media about suggested inquiry prompts related to geometric series. This article aims to share my thoughts and reflection on these prompts. Here are the prompts:

My thoughts about this geometric series

As a math expert, I know that the geometric series ½ + ¼ + 1/8 + 1/16 + ….. converges to 1. However, I have never asked myself about its significance, meaning, or even representation in real life. Additional questions came to my mind when I saw this series a few weeks ago: If the series is about adding fractions, what if we ask an upper elementary student to solve it? How can we simply represent this sum? What authentic situations use this series? How can we guide students to inquire about this series? And why does this series converge to 1?

If we ask students to find the sum of the first five terms of this series, what are the expected procedures or questions? Students may start by adding the fractions two by two. If so, they will have the following:

New questions will be raised about the pattern they observed while adding.

Since we always encourage students to represent or model their thinking, the following bars may be one of the students’ representations.

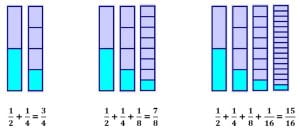
We can help students by asking them to take one whole, a square for example, and then divide it to see the given sum.

After visualizing the sum, I inquired about real-life situations to give meaning to this series. Here are two suggested word problems:

Problem 1: Jad has a square garden. He wants to water it over several days using the following strategy:

• On the first day, he waters half of his garden.
• On each next day, he waters half of the remaining dry area of the garden.

What do you think about his strategy? How many days will it take him to fully water his garden? Show your work and explain your reasoning.

Problem 2: Wissam has a yearly salary. He put a plan in place to control his expenses and save his money. His plan is as follows:

• He saves half of his salary at the end of the year.
• then, at the end of each month, he saves half of what he has left from his salary after subtracting his previous savings., he saves half of what he has left from his salary after subtracting his previous savings.

What do you think about his strategy? What fraction or percentage of this money will he save at the end of the first month? What about the second month? And the third month? A year?

 

After giving the representation, significance, and meaning of the series, teachers can start with any prompt that suits their student’s prior knowledge and ability levels and guide them through an open, structured, or guided inquiry process.

 

Reflection

Following this process of thinking, the sum of a geometric series is converted to a “low-floor, high-ceiling” math task that all students, despite background and skills, can begin and then work on at their level of engagement. This process requires teachers to have Pedagogical Content Knowledge (PCK) which involves knowing how to teach topics in ways that learners can understand, addressing misconceptions, and delivering the subject matter effectively. PCK distinguishes teachers from non-teaching specialists and involves competencies such as conceptual approach, relational understanding, and adaptive reasoning. By using inquiry prompts and real-life situations, teachers can help their students develop a deeper understanding of math concepts and foster critical thinking and problem-solving skills. As a math expert, it’s important to communicate the content effectively to students and help them become confident and competent mathematical thinkers who can apply their knowledge to solve complex problems in the real world.

In summary, whether you are a math expert or a teacher expert, you need to believe in building the bridge between Pedagogical knowledge and Content knowledge by asking why, what if, and so what. This thinking process is essential for creating effective learning experiences that meet the needs of students with different backgrounds and skill levels. With the help of Pedagogical Content Knowledge (PCK), you can effectively deliver subject matter and help your students develop deep conceptual understanding, critical thinking skills, and problem-solving skills.