Building upon the insights shared in my previous two articles about fractions: Definition & Representations and A Balanced Approach, this third piece will provide key takeaways specifically for 3-5 grade math teachers. Focusing on the essential aspects of teaching fractions, I will emphasize the importance of promoting a deep and conceptual understanding of this math concept. To help teachers achieve this goal, I will present ten questions that they can use to assess their students’ understanding of fractions, gauge students’ grasp and determine what areas may need further attention and review. Whether you are an experienced or new teacher, this article will equip you with the necessary tools to deliver effective and engaging lessons on fractions.

Teaching for Conceptual Understanding

Students often have an informal understanding of fractions before they receive instruction on fractions in school. This informal knowledge should be built upon when given meaning to formal fraction symbols and operations. (Mack, 1990). While transferring students’ prior knowledge, it is essential to focus initial instruction on building conceptual understanding because it is more difficult for students to acquire conceptual understanding once they have learned rote procedures. (Owens, 1993). Therefore, teachers need to have a deep understanding of the different meanings of fractions, knowledge about the related conceptual understandings, and the wisdom to know when and how to interfere.

In his article “Conceptual Understanding in Mathematics”, Grant Wiggins used the following definition:

Conceptual understanding in mathematics means that students understand which ideas are key (by being helped to draw inferences about those ideas) and that they grasp the heuristic value of those ideas. They are thus better able to use them strategically to solve problems – especially non-routine problems – and avoid common misunderstandings as well as inflexible knowledge and skill. (Wiggins, 2014)

 Therefore, how can we ensure that students demonstrate an understanding of all the concepts of fractions?

Rather than explaining how you can make it happen, I will share a set of 10 questions to be given to your 5th and 6th graders who have passed all the concepts related to fractions. You can also use them as guidelines to ensure that your students will reach a deep understanding of fractions.

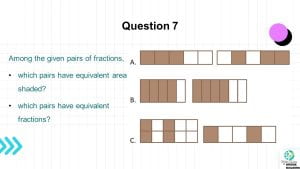
Finally, I would like to share with you some tips or advice that may guide you in your journey of teaching fractions.

• Expose learners to a variety of fractions models, including the area model and the number line, and support them to explore all the meaning of fractions through visual aids and real-life examples.
• Discuss with students what fractions are and the variety of ways in which they can be represented and used.
• Practice skip counting by fractions using the numbers line as a reference to show their strategies.
• Avoid simplistic tasks using pre-divided shapes. Instead, engage students in practical tasks using a variety of models, where they must focus on trying to make parts that are the same size.
• Challenge learners by asking them to draw or fold fractions with odd denominators.
• Ensure that students are aware of the attribute they are using to show fractions; they have to understand what is being divided into parts whether it is the area model or a line segment.
• Encourage students to think creatively when modeling fractions by using unusual, irregular, or asymmetric shapes and to evaluate the suitability of various shapes for representing particular fractions.
• Provide “non-examples” of fraction representations so students can see the difference.
• Rely on questioning and discussion as a daily routine to prompt students’ thinking and tickle their minds.
• Make discussion of strategies a regular feature of the Math session, whether the discussion happens with peers, teacher, or small group.
• Challenge learners to prove their thinking by modeling, explaining, and justifying.
• Avoid the teaching of a procedure without allowing ample opportunity to build the conceptual understanding of the taught concepts and provide them with continuous productive feedback so they can get a deep understanding of what they are doing.
• Don’t stick to one material or manipulative. Once you ensure that your students understood the meanings of fractions, help them to transfer and show their understanding using other materials, such as pattern blocks, fractions pie, fraction strips.
• Encourage kids to use mental computation when possible and give them time to think and discuss processes, and to develop an understanding of an operation, so they will be able later on to use more symbolic ways to compute.

References

Fractions Misunderstandings. (n.d.).Retrieved from https://topdrawer.aamt.edu.au/Fractions/Misunderstandings/Number-of-parts-only/Unequal-areas

Johson, Tipps, Kennedy (2017). Guiding Children’s Learning of Mathematics. Cengage Learning; 013 edition.

What Is a Fraction? Definition and Various Meanings. (2021, August 21). Retrieved from https://www.smartick.com/blog/math/number-and-operations-fractions/fraction-definition-various-meanings/

Wiggins, G. (2014). Conceptual Understanding in Mathematics [Blog post]. Retrieved from https://grantwiggins.wordpress.com/2014/04/23/conceptual-understanding-in-mathematics/